Graph Theory Definitions

This blog post is a summary and reference sheet for basic concepts encountered in graph theory. It is not meant to be exhaustive, but just to collect in one place, most of what makes an appearance in a first-semester course in graph theory.

Simple Graphs

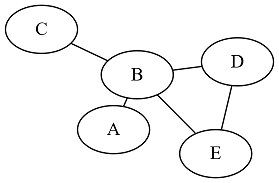
The diagram below shows a simple graph with vertices named A through E, and the edges join some of the vertices.

A simple graph (often just called a graph) is defined as a collection (set) V of vertices (also called nodes), and a collection E of edges, such that

Each edge $e\in E$ is a set of two vertices $e = \{u,v\}\subseteq V$. The vertices u, v are called the endpoints of the edge. A vertex is called incident to an edge if the vertex is an endpoint of the edge.
The endpoints of each edge are always distinct. (No self-loops.)
Between any two vertices there is at most one edge.

The vertex set is represented by $$V= \{A,B,C,D,E\}$$ and the edge set is represented by $$E = \{ \{A,B\}, \{B,C\}, \{B,D\},\{B,E\},\{D,E\}\} $$

Edges in a simple graph are un-directed.

Graphs are not distinguished by their drawings. (So for example the above graph is the same as the following graph — they have the same vertex set and edge set, so drawing them in different shapes and arrangements doesn’t change the identity of the graph.)

Let G and H be two graphs, with vertex sets $V_G,V_H$ respectively, and edge sets $E_G,E_H$ respectively. G is a subgraph of H if $V_G\subseteq V_H$ and $E_G\subseteq E_H$. If W is a subset of the vertex set $V_H$ then, informally, the induced subgraph is the subgraph with vertex set W and as many edges as possible. Formally, if G is a subgraph with vertex set W, then G is induced by W if its edge set contains every edge of H which is a subset of $V_E$. (A subgraph of the example above is one with vertex set {A,B,C} and edge set {{A,B}}. The vertex set {A,B,C} and edge set {{A,B},{B,D}} is not a subgraph because it is not a graph. It’s not a graph because not every edge is a subset of the vertex set. In particular {B,D} is not a subset of {A,B,C}. The subgraph induced by vertex set $W=\{A,B\}$ is the one with edge set {{A,B}}. )

Two vertices are adjacent if an edge runs from one to the other. (In the example, A is adjacent to B.)

Let G be a graph with vertices V and edges E. Its complement or inverse graph is the graph with vertex set V and edge set $E'$, where an edge is in $E'$ if and only if it is not in E. (Consider the graph made up of just the path A-B-C with no other vertices or edges. Its inverse graph has only the edge A-C.)

The degree of a vertex is the number of edges to which it is incident.

A graph is a complete graph if every two vertices are adjacent. (An example of a complete graph with five vertices is three diagrams down from here.)

A path or walk is a sequence of adjacent vertices. A simple path is a sequence of adjacent vertices in which no vertex occurs twice. A trail is a path in which no edge occurs twice. A closed path is a path with the same initial and terminal vertex. (In the first example, one path is C-B-D-B-A or even just a single vertex. A simple path is D-E. A trail that’s not a simple path is C-B-E-D-B-A. A closed path is A-B-A.)

The length of a path is the number of edges (or one less than the length of the sequence of vertices). (The length of B-D-E-B is 3.)

A cycle or loop usually means a closed simple path, although some authors have used it to merely be a synonym for a closed path. (In the first example, one cycle is B-D-E-B-C-B. A simple cycle is B-D-E-B.) Because a cycle is a path, the length of a cycle is already defined as the number of edges in it. A graph is called a cycle graph if the entire graph is a cycle.

A Hamiltonian path is a simple path that visits every vertex. A Hamiltonian cycle is a cycle that visits every vertex. A graph is called Hamiltonian if contains a Hamiltonian path, and traceable if it contains a Hamiltonian cycle. (The first example above is not Hamiltonian, nor are the next two examples below. The complete graph of five vertices, the third example down from here, is Hamiltonian.)

An Eulerian trail is a trail that visits every edge. An Eulerian cycle (or circuit) is a cycle A graph is Eulerian if it contains an Eulerian trail. (The example above is Eulerian with one Eulerian trail being A-B-D-E-C. The example below is not Eulerian.)

A vertex u can reach a vertex v if there is a path from u to v, and the two vertices are said to be reachable from each other.

A graph is called connected if every two vertices reach each other. Otherwise it is called disconnected. (The example above is connected. The example below is not.)

A collection of vertices $ C\subseteq V$ is called a connected component if it is a maximal connected subgraph — i.e. a connected subgraph not contained in any larger connected subgraph. (In the example above, {A,B} is a connected component but {A} is not.)

A graph is called a tree if it is connected and contains no cycles. If a vertex of a tree has degree at most 1, it’s called a leaf vertex, and otherwise is called internal.

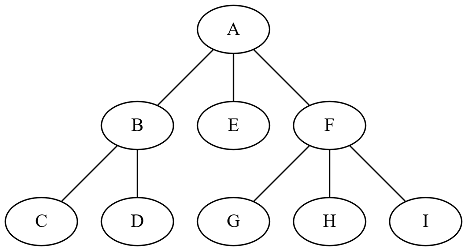
If G is a subgraph of H and G is a tree containing all of the vertices of H, then G is called a spanning tree for H. (The first example is not a tree because it contains cycles. The second example is not a tree because it is disconnected. The example below is a tree and its internal vertices are A, B, and F.)

A graph is called bipartite if there are two subsets of vertices $ A,B\subseteq V$ which partition V (i.e. every vertex is in precisely one of A or B) and no edge is incident to two vertices in the same subset. (The first example is not bipartite, but the last two are. In the second graph, we can let the first subset be {A,C} and the second {B,D}. In the tree immediately above, let the first subset be {A,C,D,G,H,I} and the second {B,E,F}.)

A graph is called planar if its drawing is equivalent to some drawing in which the edges do not cross. (Every example above is planar. The following complete graph of five vertices is not planar.)

A matching of a graph is a subset of the edge set, $M\subseteq E$, such that any two edges in M are not incident to the same vertices. For a given matching, a vertex is called matched if it is incident to some edge. Otherwise it is called unmatched. (The graph below shows a matching of the graph above, in which only E is unmatched.)

For any two graphs G and H, let $\varphi:V_G\to V_H$ be any function. If for every two vertices $a,b\in V_G$ these are incident if and only if $\varphi(a),\varphi(b)$ are incident in H, then we call $\varphi$ a graph homomorphism. If $\varphi $ is a bijective homomorphism then it is a graph isomorphism. If there is an isomorphism between two graphs, then they are called isomorphic. (There is no graph isomorphism between the graph above and the complete graph of five vertices. However, the above graph is isomorphic to the graph below. Namely $\varphi(A)=2,\varphi(B)=5,\varphi(C)=1,\varphi(D)=4,\varphi(E)=3$.)

A graph coloring is a function $\chi:V\to C$ where C is any set, but usually taken to be a set of colors (or, if you prefer, letters standing for colors). For any vertex u, its color is $\chi(u)$. An edge coloring is a function $\chi:E\to C$ for any set C. A k-coloring is a coloring for which $|C|=k$ where $|C|$ denotes the cardinality (size) of C.

A graph is called a weighted graph if it is paired with a weight function, which is any function $w:E\to \Bbb R$. We define the weight of the graph G to be the sum of all the weights on each edge, and is denoted $w(G)$.

If G is a graph with spanning tree T such that for every other spanning tree S we have $w(T)\le w(S)$ then we call T the minimum spanning tree.

A tree is called a rooted tree if it is paired with a particular vertex from its vertex set, r, called its root. Any vertex of a tree can be “made” the root vertex. The child relation on vertices is defined inductively from the root. Every vertex adjacent to the root is a child of the root. If u is any vertex adjacent to vertex v, and u is not a child of v, then v is a child of u. u is the parent of v if v is a child of u. u is an ancestor of v if there is a path from u to v such that every vertex in the path is the parent of the next vertex in the path. u is a descendant of v if v is an ancestor of u.

For any rooted tree, its height is the length of the longest simple path in it, which has its initial node at the root. The level of a node is defined inductively from the root: The root is at level zero. If u is any vertex at level n and v is a child of u, then v is at level n+1. A rooted binary tree is a rooted tree such that every vertex has at most two children.

Digraphs

A digraph (short for “directed graph”) is a vertex set and directed edge set E such that

Every edge $e\in E$ is some pair of vertices $e=(u,v)$. The vertex u is called the initial point and v is called the terminal point. We also say that v is the successor of u, and u is the predecessor of v.
For any pair of vertices, u, v, there is at most one edge from u to v.

Note that a digraph allows self-loops. That is to say, in a digraph it is possible to have an edge from a vertex to itself.

Many of the same ideas from a graph carry over to a digraph, except those that assume “symmetry” of the edges. For instance we cannot merely talk about connectivity, since it is possible for vertex u to reach v but not vice versa. Therefore we call a graph strongly connected if every vertex can reach every other vertex, but weakly connected if there is some vertex which can reach every other vertex. A strongly connected component is a sub-digraph which is strongly connected and not contained within any larger strongly connected sub-digraph.

Vertices do not merely have degrees but instead have in-degree and out-degree. If v is a vertex, its in-degree is the number of edges with terminal point v. Its out-degree is the number of edges with initial point v. A vertex is called a source if its in-degree is zero, and is called a sink if its out-degree is zero.

A digraph is called reflexive if every vertex has a self-loop. A digraph is called symmetric if, whenever u is a predecessor of v, then u is also a successor of v. A digraph is called transitive if, whenever u-v and v-w, then also u-w.

Multigraphs

A multigraph is most easily understood as being “like a graph”, but allowing many different edges between vertices, and also allowing self-loops. As such we need a way to distinguish the edges other than by their endpoints, and therefore we require some kind of label (often letters or words) on the edges.

Formally this is accomplished by saying that there is a function from a label set (which is any set of elements) to the set of all two-element subsets of V. An edge is then any label together with the vertices that are associated with the label.

Graph Theory Basics

Graph Theory Definitions

Simple Graphs

Digraphs

Multigraphs